错题本 | LeetCode703. 数据流中的第 K 大元素

不是吧啊Sir，这种题也错？😢

题目链接：https://leetcode-cn.com/problems/kth-largest-element-in-a-stream/

题目

设计一个找到数据流中第 k 大元素的类（class）。注意是排序后的第 k 大元素，不是第 k 个不同的元素。

请实现 KthLargest 类：

KthLargest(int k, int[] nums) 使用整数 k 和整数流 nums 初始化对象。

int add(int val) 将 val 插入数据流 nums 后，返回当前数据流中第 k 大的元素。

示例1

输入： [“KthLargest”, “add”, “add”, “add”, “add”, “add”] [[3, [4, 5, 8, 2]], [3], [5], [10], [9], [4]]

输出： [null, 4, 5, 5, 8, 8]

示例2

输入： [“KthLargest”,“add”,“add”,“add”,“add”,“add”] [[2,[0]],[-1],[1],[-2],[-4],[3]]

输出： [null,-1,0,0,0,1]

分析

啪地一下，我就想到了双堆对顶，很快嗷！

然而又想复杂了o(╥﹏╥)o。要求第K大数，实际上只需要使用一个小根堆，堆中一共有K个元素，堆顶就是目标。

当然，这K个元素不是随随便便的K个元素，而是将初始数组中所有元素都放入小根堆后，逐个弹出，直到只剩K个元素。

当我们希望添加元素时，首先可以比较此元素与堆顶元素的大小关系，当此元素比堆顶元素小时，不会对前K个大数的顺序产生影响，直接返回堆顶元素即可；当此元素大于堆顶元素，第K大数一定会改变，我们将其放入堆中，再从堆中弹出一个元素，此时的堆中还是K个元素，堆顶元素即为答案。

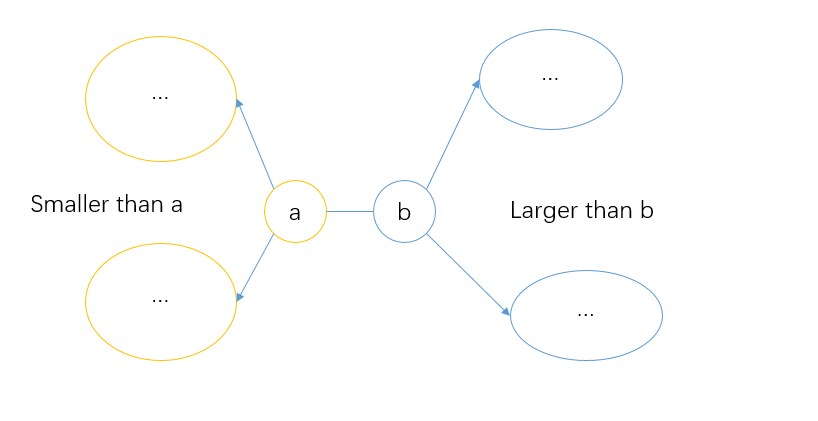
我最开始的想法，双堆对顶又是什么呢？这是一种同时使用小根堆和大根堆来维护整个数组的办法，小根堆larger中的所有元素都比堆顶元素更大，大根堆smaller中的所有元素都比堆顶元素小。这样，任何时刻，数组中的数据被组织如下：

双堆对顶

这种办法可以用于快速求解数据流的中位数，是个困难题，我还没做。根据中位数的定义，中间部分的数据正需要满足比左边都大，比右边都小的性质，使用双堆对顶的办法可以在 O(1) 的时间内找到数据流中的中位数。

这题使用双堆对顶是杀鸡用了牛刀了。将小于第K大数的数据保存在smaller堆中并没有什么意义，只是空耗时间罢了。

而且，这种办法在额外考虑初始数组为空的情况、以及初始数组的大小小于K的情况时比较繁琐，我在这里WA了两次😢

AC代码1

class KthLargest {
public:
    priority_queue<int, vector<int>, greater<int>> larger;
    priority_queue<int, vector<int>, less<int>> smaller;
    bool larger_not_full = true;
    // larger是个小顶堆，堆顶元素是最小的
    // smaller是个大顶堆，堆顶元素是最大的
    // 第K大数，表示有K - 1个数比他更大
    // 有len - K个数比他更小
    // e.g 4,5,8,2中的第三大数
    // 有两个比他小，有一个比他大
    // 我们以larger.top()为第K大数，则smaller里面始终保持len - K个元素
    KthLargest(int k, vector<int>& nums) {
        if (nums.size() == 0)
            nums.push_back(-100000);  // 放入一个极小值，对第K大数无影响
        for (auto t : nums)
        {
            larger.push(t);
        }
        if (nums.size() >= k)
        {
            for (int i = 0; i < nums.size() - k; i++)
            {
                smaller.push(larger.top());
                larger.pop();
            }
            larger_not_full = false;
        }
        // larger里的所有元素都大于堆顶
        // 故保持larger个数为K个，即可从堆顶中获取第K大数
        // cout << "Original " << k << "th. largest is " << larger.top() << endl;
    }


    int add(int val) {
        int res;
        if (larger_not_full)
        {
            larger.push(val);
            res = larger.top();
            larger_not_full = false;
        }
        else
        {
            if (val >= larger.top())  // 比第K大数还大，第K大数可能改变
            {
                smaller.push(larger.top());
                larger.pop();
                larger.push(val);
                // cout << larger.top() << endl;
                res = larger.top();
            }
            else  // 插入了一个更小的数，不会改变第K大数
            {
                smaller.push(val);
                // cout << larger.top() << endl;
                res = larger.top();
            }
        }
        return res;
    }
};

/**
 * Your KthLargest object will be instantiated and called as such:
 * KthLargest* obj = new KthLargest(k, nums);
 * int param_1 = obj->add(val);
 */

AC代码2

class KthLargest {
public:
    priority_queue<int, vector<int>, greater<int>> larger;
    int K;
    KthLargest(int k, vector<int>& nums) {
        K = k;
        for (auto t : nums)
        {
            larger.push(t);
        }
        while (larger.size() > k)
        {
            larger.pop();
        }
        // larger里的所有元素都大于堆顶
        // 故保持larger个数为K个，即可从堆顶中获取第K大数
        // cout << "Original " << k << "th. largest is " << larger.top() << endl;
    }

    int add(int val) {
        int res;
        if (larger.size() < K)
        {
            larger.push(val);
            res = larger.top();
        }
        else
        {
            if (val >= larger.top())  // 比第K大数还大，第K大数可能改变
            {
                larger.push(val);
                larger.pop();
                res = larger.top();
            }
            else  // 插入了一个更小的数，不会改变第K大数
            {
                res = larger.top();
            }
        }
        return res;
    }
};

/**
 * Your KthLargest object will be instantiated and called as such:
 * KthLargest* obj = new KthLargest(k, nums);
 * int param_1 = obj->add(val);
 */

优化掉smaller堆之后，表现会好一些。

参考资料

[1] 力扣官方题解.数据流中的第K大元素[EB/OL].2021-02-11

https://leetcode-cn.com/problems/kth-largest-element-in-a-stream/solution/shu-ju-liu-zhong-de-di-k-da-yuan-su-by-l-woz8/