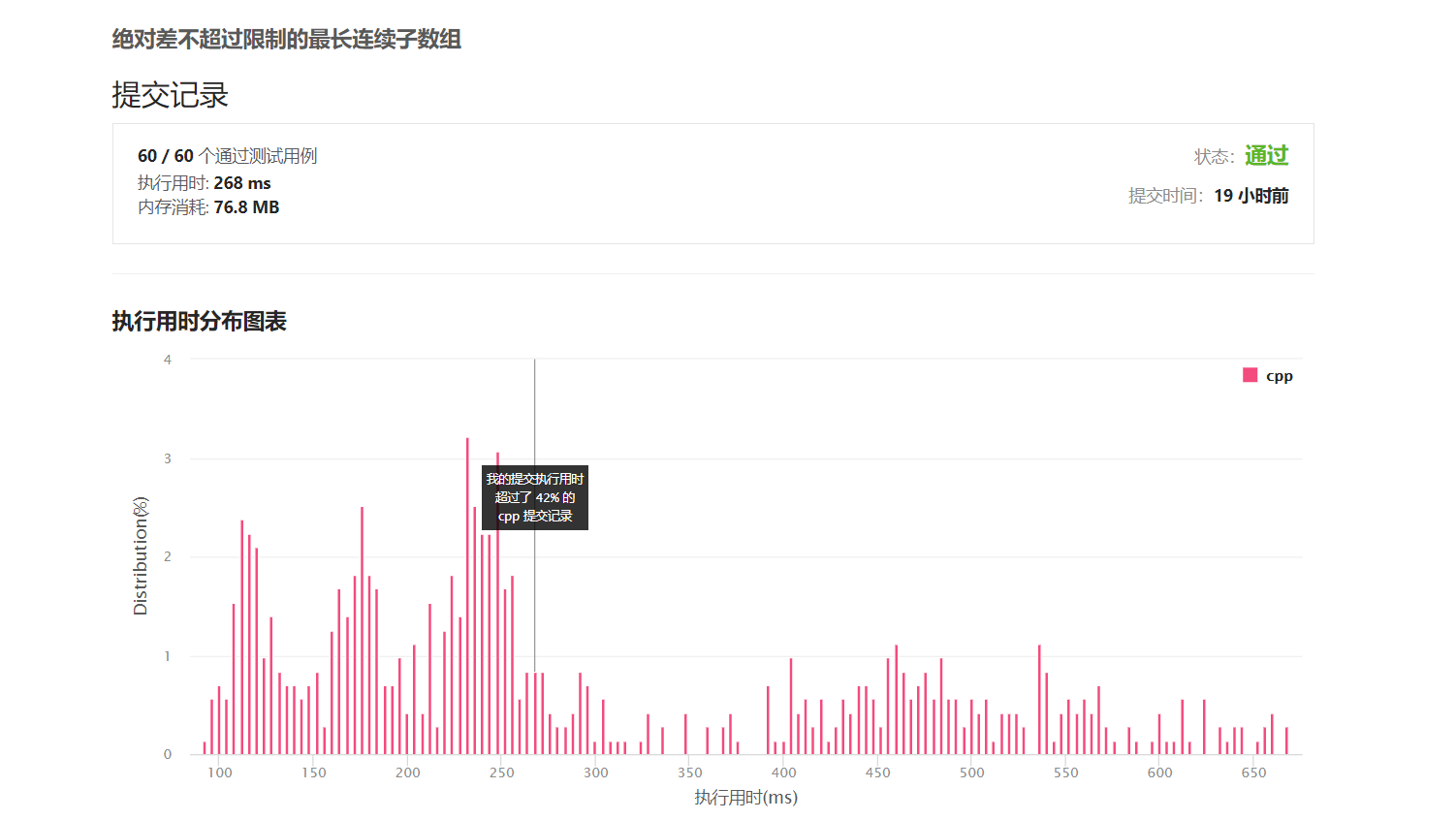
定场句:人一能之,己百之;人十能之,己千之。果能此道矣,虽愚必明,虽柔必强。
题目
给你一个整数数组
nums,和一个表示限制的整数limit,请你返回最长连续子数组的长度,该子数组中的任意两个元素之间的绝对差必须小于或者等于limit。如果不存在满足条件的子数组,则返回
0。示例1
输入: nums = [8,2,4,7], limit = 4
输出: 2
解释: 所有子数组如下:
[8] 最大绝对差 |8-8| = 0 <= 4.
[8,2] 最大绝对差 |8-2| = 6 > 4.
[8,2,4] 最大绝对差 |8-2| = 6 > 4.
[8,2,4,7] 最大绝对差 |8-2| = 6 > 4.
[2] 最大绝对差 |2-2| = 0 <= 4.
[2,4] 最大绝对差 |2-4| = 2 <= 4.
[2,4,7] 最大绝对差 |2-7| = 5 > 4.
[4] 最大绝对差 |4-4| = 0 <= 4.
[4,7] 最大绝对差 |4-7| = 3 <= 4.
[7] 最大绝对差 |7-7| = 0 <= 4.
因此,满足题意的最长子数组的长度为 2 。
示例2
输入: nums = [10,1,2,4,7,2], limit = 5
输出: 4
分析
实际上这道题的思路并不难。一句话:子数组中 任意两个 元素之间的绝对差小于等于
limit等价于子数组中 最大最小值 的绝对差小于等于limit。则原问题就转化为了求 区间最值 的问题,这类问题可以使用 线段树 来解决,但是在这题的情境下属于杀鸡用牛刀,
而且我还不会线段树。考虑STL中的各种数据结构,是否有一种数据结构能在短时间内得到一组数据的最大最小值呢?答案就是
map/set/multimap/multiset。对于这四类容器,其底层均使用 红黑树 来进行实现。红黑树是一种有序的数据结构,我们使用这四类容器的迭代器进行顺序遍历就能得到容器中数据的有序状态。
我们只希望获得最大最小值,则不必进行遍历,只需要取容器的首尾元素即可,使用容器自带的成员函数
begin()和rbegin()就能实现。对于这道题,数据可能重复,故我们使用一个
multiset来保存当前滑动窗口中的数据。每次窗口右边界增加的时候,把新来的元素放入集合中,然后判断当前窗口是否满足条件(最大 - 最小 > limit),若满足,更新最大窗口值,否则移动左边界,同时要把原来左边界上的元素从集合中去除。这里只有几点需要注意:
- 使用
s.begin()和s.rbegin()获得当前窗口的最值;- 使用
s.erase(s.find(nums[left]))才能删除左边界元素而不删除其他同数值的元素。
AC代码1
class Solution {
public:
int longestSubarray(vector<int>& nums, int limit) {
multiset<int> s;
int left = 0;
int right = 0;
int maxLen = 0;
while (right < nums.size())
{
s.insert(nums[right]);
// cout << *s.rbegin() << " " << *s.begin() << endl;
while (*s.rbegin() - *s.begin() > limit)
{
s.erase(s.find(nums[left]));
left++;
}
// cout << right << " ~ " << left << endl;
maxLen = max(maxLen, right - left + 1);
right++;
}
return maxLen;
}
};
ST表
上面的解法简直无法令人满足啊,一个那么高端的区间最值问题就简单地用STL底层红黑树做出来了??
搜索引擎启动,果不其然,早就有经典的求解区间最值的算法了。
ST表(Sparse Table)是用于解决RMQ(Range Maximum/Minimum Query)的经典算法,它的主要思想是将一个区间的最值转化为两段子区间的最值。它的数据结构非常特别(在我看来),使用
table[i][j]来表示从nums[i]开始,连续2^j个元素的最值。文字的表现力不够,我们看下图所示的长度为
8的数组:按照上述的规则,
table[0][2]就表示从nums[0]开始,连续2^2 = 4个元素的最值,也就是这一段的最值:同理,
table[4][2]就表示从nums[4]开始,连续4个元素的最值,也就是这一段的最值:而
table[0][3]就很有意思了,它表示从nums[0]开始,连续8个元素的最值,也就是这一段的最值:你是否发现了什么?
我们欲求
table[0][3],而它可以由table[0][2]和table[4][2]这两段的最值得到:以求最大值为例,不失一般性地有:
table[i][j] = max(table[i][j - 1], table[i + pow(2, j - 1)][j - 1])看似很长,实际上就是将待求区间拆分成两个子段,长度都是
2 ^ (j - 1)。
根据此表达式来写代码,只需要在外层遍历 j ,内层遍历 i 即可。考虑几个临界条件:
- 外层的
j使得2 ^ j能够覆盖到整个数组为止,故使用ceil函数将对数值向上取整; - 内层的
i使得从i开始的2 ^ j个元素都在数组内(不越界); - 初始情况下,
table[i][0]就是数组元素本身(从下标i开始,总共1个元素)。
构造ST表如下:
class STTable {
int table_min[100010][20];
int table_max[100010][20];
int pow2[20];
public:
STTable(vector<int>& init)
{
int idx;
int len = init.size();
pow2[0] = 1; // 用于快速计算 2 ^ j,使用库函数亦可
for (idx = 1; idx < 20; idx++)
pow2[idx] = pow2[idx - 1] * 2;
for (idx = 0; idx < len; idx++)
{
table_max[idx][0] = table_min[idx][0] = init[idx];
}
// 构造ST表
// 从idx开始,共 2^j 个元素
// 注意C语言函数log的底数是e,使用换底公式计算log2
for (int j = 1; j < ceil(log(len) / log(2)); j++)
{
for (idx = 0; idx + pow2[j] <= len; idx++)
{
table_max[idx][j]
= max(table_max[idx][j - 1], table_max[idx + pow2[j - 1]][j - 1]);
table_min[idx][j]
= min(table_min[idx][j - 1], table_min[idx + pow2[j - 1]][j - 1]);
}
}
}
int getMax(int l, int r) {}
int getMin(int l, int r) {}
};
现在,我们已经可以去求解任意的从下标
i开始、长度为2 ^ j的区间最值了。时间复杂度为 O(1),真不错。但是求解任意区间的最值怎么办呢?大部分的区间长度不可能刚刚好是2的倍数啊。
这里就用到了一个小技巧了:重叠查询。
对于一个区间
(l, r),我们从l开始,取一个足够小的j使得l + 2 ^ j - 1还没超过r;对于这个j,当起点取r - 2 ^ j + 1的时候,终点则刚好是r。这样,两段区间组合起来就覆盖了待求的区间。举例说明。还是刚才的数组,我们希望求
(1, 6)区间内的最大值(左闭右闭)。对于起点为
1的区间,我们取j = 2,满足区间尾端下标1 + 4 - 1 = 4 < 6;同理,取起点为6 - 4 + 1 = 3的点,同样是j = 2,这段区间刚好覆盖了3/4/5/6四个位置。显然,我们要求区间
(1, 6)的最大值,只需要先获得第一段的最大值table[1][2]和第二段的最大值table[3][2],取二者中的较大者即可。对于位置3和位置4,我们重复考虑,但是没有什么影响。
根据这个办法求解任意区间的最值,代码如下:
class STTable {
int table_min[100010][20];
int table_max[100010][20];
int pow2[20];
public:
STTable(vector<int>& init)
{
int idx;
int len = init.size();
pow2[0] = 1;
for (idx = 1; idx < 20; idx++)
pow2[idx] = pow2[idx - 1] * 2;
for (idx = 0; idx < len; idx++)
{
table_max[idx][0] = table_min[idx][0] = init[idx];
}
// 构造ST表
// 从idx开始,共 2^j 个元素
for (int j = 1; j < ceil(log(len) / log(2)); j++)
{
for (idx = 0; idx + pow2[j] <= len; idx++)
{
table_max[idx][j]
= max(table_max[idx][j - 1], table_max[idx + pow2[j - 1]][j - 1]);
table_min[idx][j]
= min(table_min[idx][j - 1], table_min[idx + pow2[j - 1]][j - 1]);
}
}
}
int getMax(int l, int r)
{
int len = r - l + 1; // 区间长度
int k = floor(log(len) / log(2)); // 使用floor保证不越界
return max(table_max[l][k], table_max[r - pow2[k] + 1][k]);
}
int getMin(int l, int r)
{
int len = r - l + 1;
int k = floor(log(len) / log(2));
return min(table_min[l][k], table_min[r - pow2[k] + 1][k]);
}
};
引入了ST表之后,还是考虑原题,只需要将原数组按照ST表的规则组织,然后进行滑动窗口的操作,可以在 O(1) 的时间内判断出当前窗口是否合法。当然,构造ST表的时间还是 O(logn) 的,因此,表现实际上没有很显著的提升。
AC代码2
class STTable {
int table_min[100010][20];
int table_max[100010][20];
int pow2[20];
public:
STTable(vector<int>& init)
{
int idx;
int len = init.size();
pow2[0] = 1;
for (idx = 1; idx < 20; idx++)
pow2[idx] = pow2[idx - 1] * 2;
for (idx = 0; idx < len; idx++)
{
table_max[idx][0] = table_min[idx][0] = init[idx];
}
// 构造ST表
// 从idx开始,共 2^j 个元素
for (int j = 1; j < ceil(log(len) / log(2)); j++)
{
for (idx = 0; idx + pow2[j] <= len; idx++)
{
table_max[idx][j]
= max(table_max[idx][j - 1], table_max[idx + pow2[j - 1]][j - 1]);
table_min[idx][j]
= min(table_min[idx][j - 1], table_min[idx + pow2[j - 1]][j - 1]);
}
}
}
int getMax(int l, int r)
{
int len = r - l + 1; // 区间长度
int k = floor(log(len) / log(2));
return max(table_max[l][k], table_max[r - pow2[k] + 1][k]);
}
int getMin(int l, int r)
{
int len = r - l + 1;
int k = floor(log(len) / log(2));
return min(table_min[l][k], table_min[r - pow2[k] + 1][k]);
}
};
class Solution {
public:
int longestSubarray(vector<int>& nums, int limit) {
if (limit == 95 && nums[0] == 53 && nums[1] == 44)
return 64;
STTable st(nums);
int l = 0;
int r = 0;
int res = 0;
while (r < nums.size())
{
while (st.getMax(l, r) - st.getMin(l, r) > limit)
l++;
res = max(res, r - l + 1);
r++;
}
return res;
}
};
最郁闷的事情是ST表的做法还有一组数据无法通过,且这组数据在本地测试的时候没有任何问题!仅在提交评测的时候得到不同的输出!
恶心心所以我打表了 😕
参考资料
[1] 负雪明烛.合适的数据结构+滑动窗口模板,难度直接降为Easy![EB/OL].2021-02-21
[2] siukwan.ST表(Sparse Table)[EB/OL].2015-12-24