题目链接:https://leetcode-cn.com/problems/implement-trie-prefix-tree/
定场句:人一能之,己百之;人十能之,己千之。果能此道矣,虽愚必明,虽柔必强。
题目
Trie(发音类似 “try”)或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。请你实现
Trie类:
Trie()初始化前缀树对象。
void insert(String word)向前缀树中插入字符串word。
boolean search(String word)如果字符串word在前缀树中,返回true(即,在检索之前已经插入);否则,返回false。
boolean startsWith(String prefix)如果之前已经插入的字符串word的前缀之一为prefix,返回true;否则,返回false。示例
输入:
[“Trie”, “insert”, “search”, “search”, “startsWith”, “insert”, “search”]
[[], [“apple”], [“apple”], [“app”], [“app”], [“app”], [“app”]]
输出:
[null, null, true, false, true, null, true]
解释:
Trie trie = new Trie();
trie.insert(“apple”);
trie.search(“apple”); // 返回 True
trie.search(“app”); // 返回 False
trie.startsWith(“app”); // 返回 True
trie.insert(“app”);
trie.search(“app”); // 返回 True
数据范围:
1 <= word.length, prefix.length <= 2000
word和prefix仅由小写英文字母组成
insert、search和startsWith调用次数 总计 不超过30000次
分析
是一个全新的知识点呢 (#^.^#)
前缀树 Trie 是一种高效的用于信息检索(information retrieval)的数据结构,可以将搜索复杂度降到最低(关键字长度)。如果我们要在一堆字符串中寻找一个子串,常见的使用 二分搜索树 的思路时间复杂度为 O(M * log N) ,其中 M 是最长子串的长度,N 是现有的字符串个数。而使用前缀树,时间复杂度可以降为 O(M) 。
原理 —— 插入
前缀树是一颗 多叉树 ,它的每一个节点可以分出若干个子节点,每一条边表示一个字符。你可以发现,从根节点开始向下走去,每走过一条边我们就得到了一个字符,遍历到一个 终止节点 时,我们就得到了一个 单词(字符串) 。
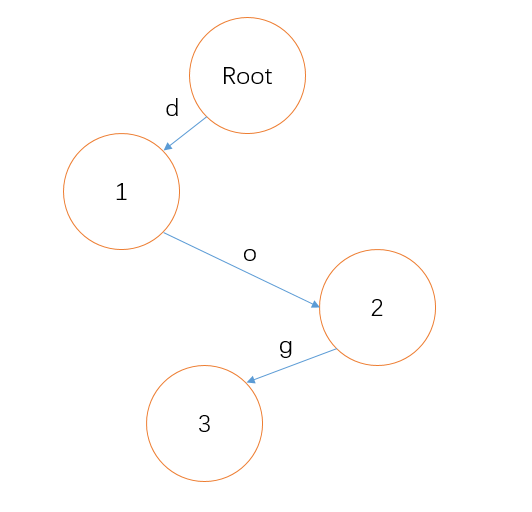
比如,单词 dog 就能组成这么一颗前缀树:
从根节点向下遍历,到了节点 3 ,它应该被标记为 终止节点 ,我们就得到了 dog 。
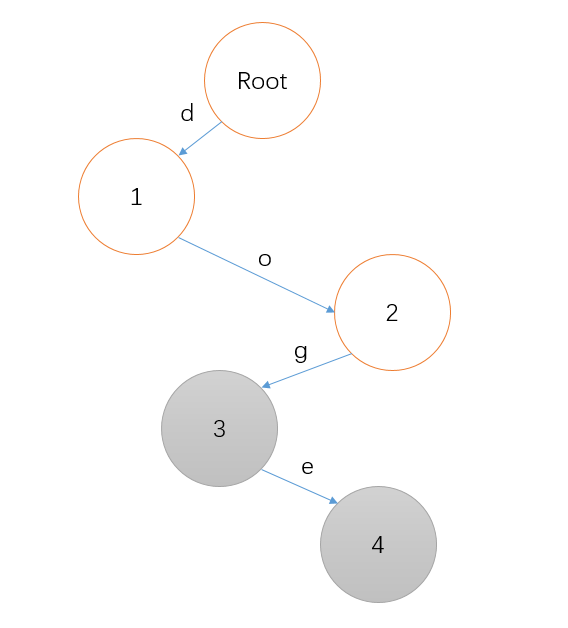
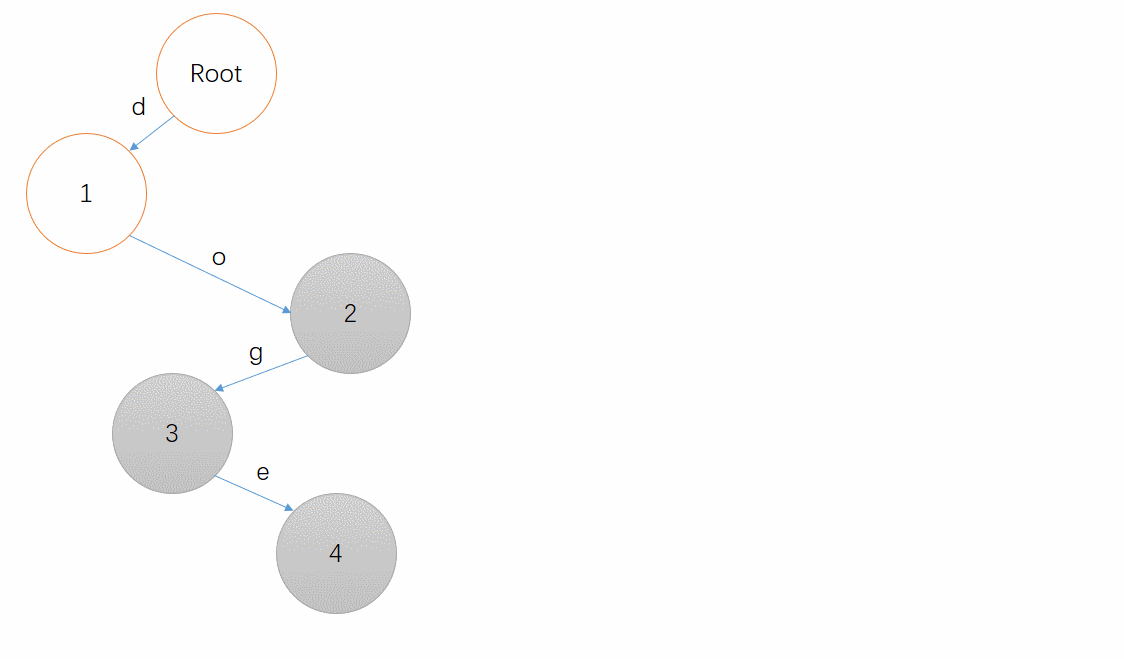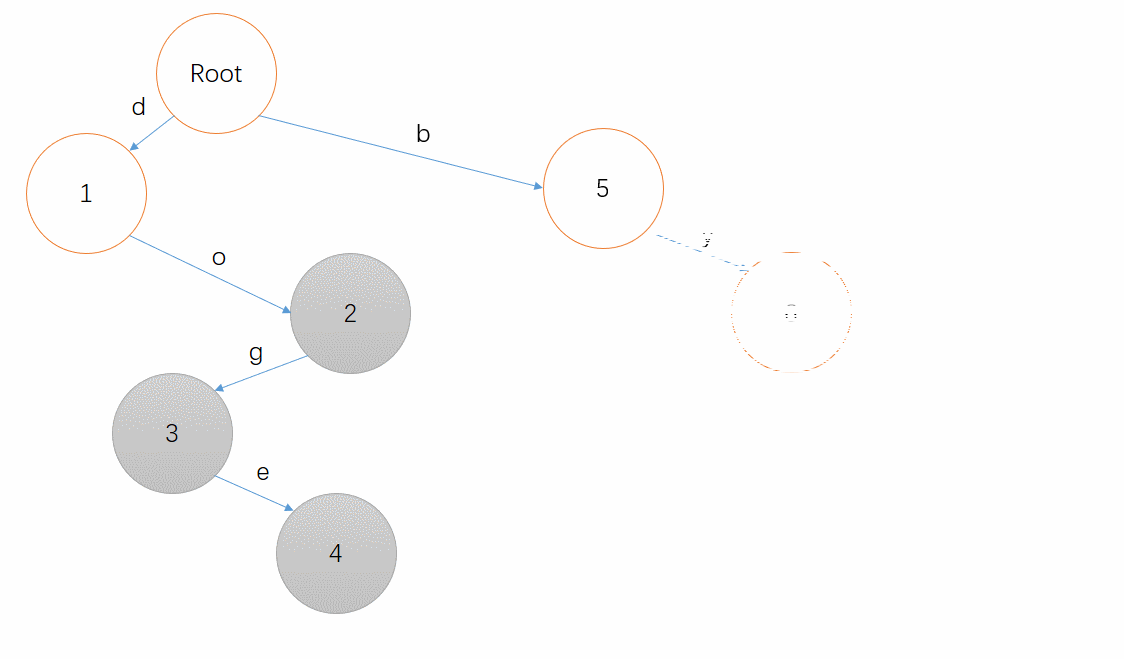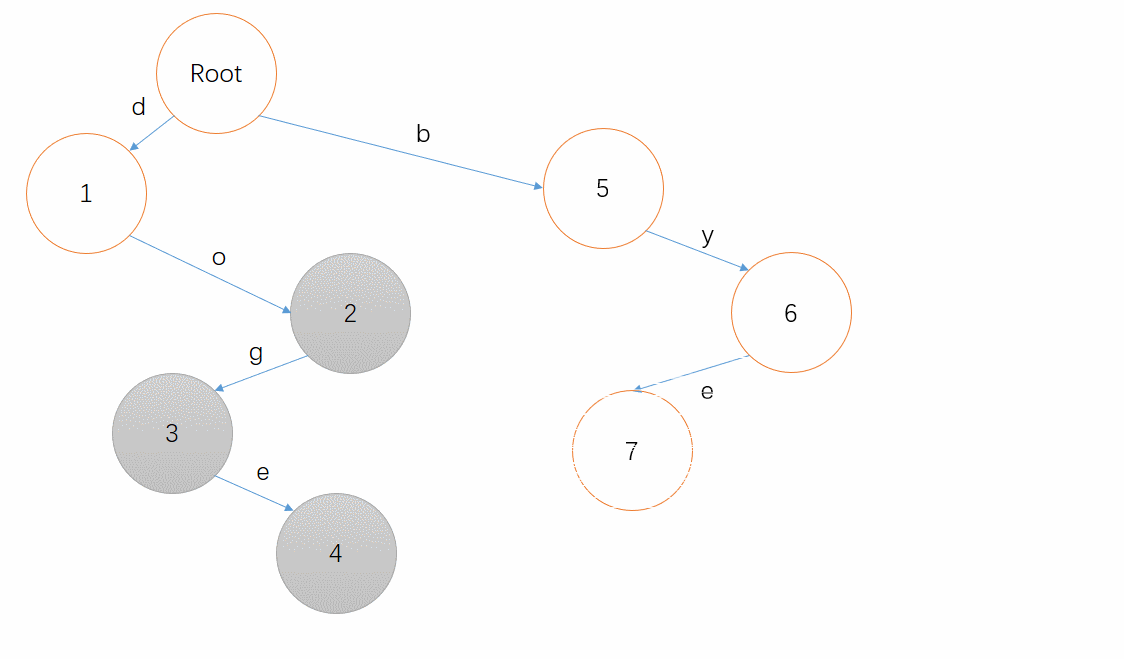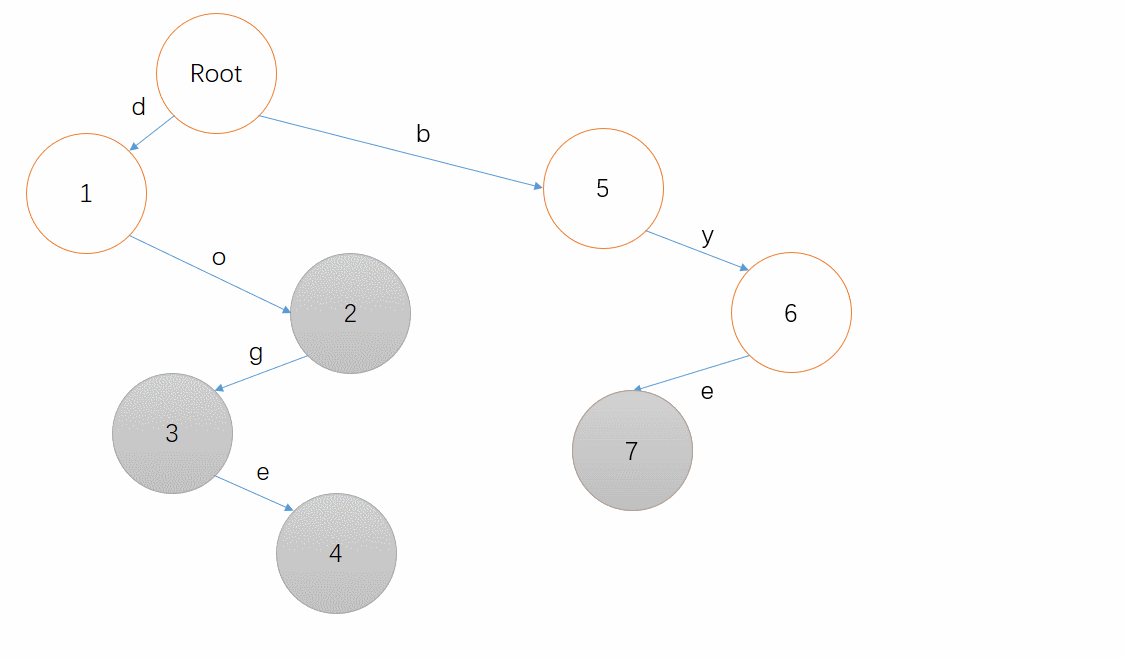
现在我们希望插入一个单词 doge ,要怎么做呢?
我们还是进行遍历,从根节点出发,依次获取 d 、 o 、 g ,来到了节点 3 ,只需要再插入一条边表示 e 就可以了!
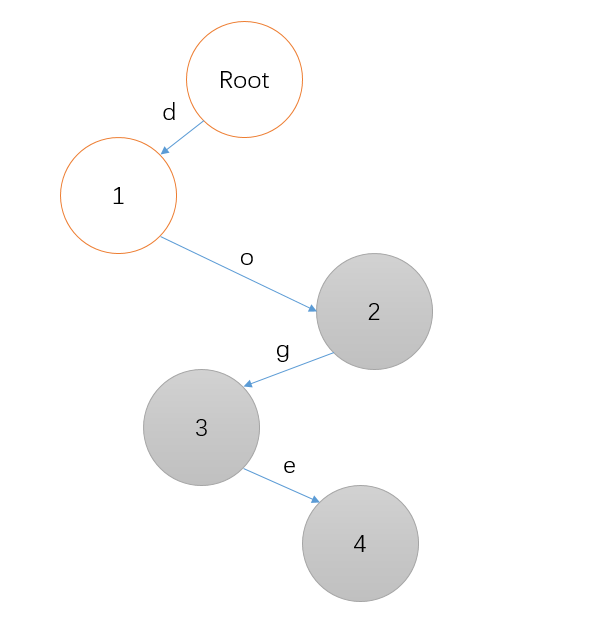
在上面的图中,我标出了 终止节点 ,当我们遍历到 3 或 4 时,我们知道它们表示的是一个切实存在的字符串;而当我们遍历到 2 或 1 时,我们知道 do 或者 d 不是一个切实存在的字符串,它们只是某个单词的前缀而已。
从这个模拟中可以看到, doge 和 dog 使用的是同一些字母前缀,这就是 前缀树 的意思。
我们再插入一个单词 do ,这时根据我们遍历的结果发现,到达节点 2 的路径就能表示这个单词!那么我们不用再申请一个新的节点,直接将 2 标记为 终止节点 即可。
最后,插入一个 bye 吧,相信读者已经能够模拟出这个过程了!(也可以点开下面的动图看看答案)
原理 —— 查询
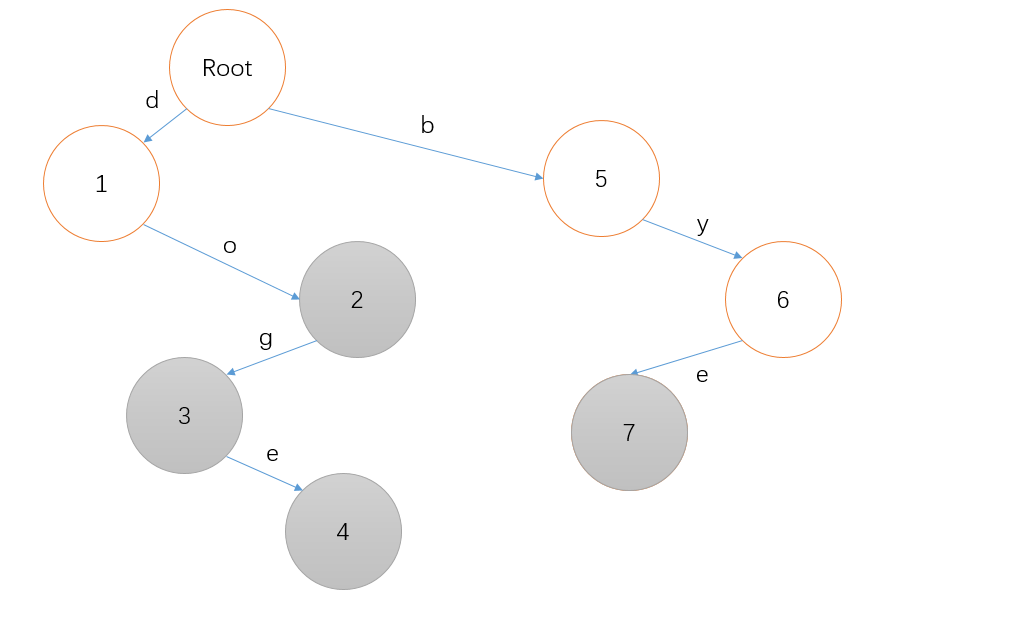
我们能够插入一个单词(字符串),当然也就需要能够查询某个单词。对于一个给出的字符串 s ,我们从 Trie 的根节点出发,沿着它的每一个字符向下遍历,如果能够到达一个 终止节点 ,那么这个字符串 s 就存在于我们的集合中,否则它就是不存在的。
例如我们要查询单词 bye ,从根节点出发,沿着每个字符对应的路径依次来到了 5 、 6 、 7 ,最后我们发现节点 7 是个终止节点,太好了,这个单词就是存在的。
而当我们要查询单词 by ,从根节点出发,依次来到 5 、 6 ,节点 6 不是终止节点,那么这个单词就不存在于我们的集合中。
原理 —— 构造
现在,我们能够将一个单词插入 Trie 中,也能查询一个单词是否存在于 Trie 中了,最后的问题是,如何构造这颗前缀树呢?
从上面的例子中,你应该想到,这颗前缀树应该是一颗 多叉树 ,正如一开始所说的那样,而且,它每一个节点所分出来的边必须能够表示我们的 字符集 ,也就是说,假如我们的字符集记做 Σ ,那么前缀树的每个节点就应该有 len(Σ) 数量的边。在这道题中(你可能已经忘了题目了~),每个节点分出来的边数量就是 26 ,表示 a ~ z 是也。
方法一
如果我们对节点进行编号,就可以用一个 二维数组 来保存整个 Trie 了,我们声明一个 trie[NODE_NUM][26] ,第一个下标表示节点编号,第二个下标表示分出来的26条边,每个边表示一个字母。
如何表示终止节点呢?很简单,再声明一个 mark[NODE_NUM] 即可,对于任意一个节点的编号 p ,当 mark[p] 为 1 的时候表示它是终止节点。
根节点编号是 0 ,对于我们上面的例子来说,bye 这个单词对应的路径是这样的:
trie[0][1] = 5trie[5][24] = 6trie[6][4] = 7
每一个字符 ch 对应的第二个下标就简单地用 ch - 'a'来表示就行了。
方法二
第一种构造方法胜在简单,节点下标和延伸出的边含义很直观,但是所耗费的空间比较大,即使某条路径是不存在的(如单词 hello ),它所对应的空间还是存在于数组中(只不过都被写为了 0 来表示不存在)。
如果我们用链表的思想 + 动态申请内存的办法,效果则大不相同。使用一个数据结构来表示节点,它含有一个长度为 26 的 指针数组 ,每一个单元表示对应的边,指向下一个节点。同时,这个结构顺便定义了一个成员变量来表示该节点是否为终止节点,这种办法就简洁多了。
AC代码1
此代码对应构造方法1
class Trie {
public:
int tire[100000][26];
int mark[100000];
int k;
/** Initialize your data structure here. */
Trie() {
k = 1;
memset(tire, 0, sizeof(tire));
memset(mark, 0, sizeof(mark));
}
/** Inserts a word into the trie. */
void insert(string word) {
int p = 0;
int c = 0;
for (auto ch : word)
{
c = ch - 'a';
if (tire[p][c] != 0)
{
p = tire[p][c];
}
else
{
tire[p][c] = k; // 编号从1开始
k++;
p = tire[p][c];
}
}
mark[p] = 1;
}
/** Returns if the word is in the trie. */
bool search(string word) {
int p = 0;
int c = 0;
for (auto ch : word)
{
c = ch - 'a';
if (tire[p][c] != 0)
{
p = tire[p][c];
}
else
{
return false;
}
}
if (mark[p])
return true;
else
return false;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
bool startsWith(string prefix) {
int p = 0;
int c = 0;
for (auto ch : prefix)
{
c = ch - 'a';
if (tire[p][c] != 0)
{
p = tire[p][c];
}
else
{
return false;
}
}
return true;
}
};
/**
* Your Trie object will be instantiated and called as such:
* Trie* obj = new Trie();
* obj->insert(word);
* bool param_2 = obj->search(word);
* bool param_3 = obj->startsWith(prefix);
*/
AC代码2
此代码对应构造方法2
class Trie {
public:
typedef struct n {
struct n* childen[26];
int mark;
} Node, *PNode;
PNode root;
/** Initialize your data structure here. */
Trie() {
root = new Node;
for (int i = 0; i < 26; i++)
{
(*root).childen[i] = 0;
}
}
/** Inserts a word into the trie. */
void insert(string word) {
PNode p = root;
int c = 0;
for (auto ch : word)
{
c = ch - 'a';
if ((*p).childen[c])
{
p = (*p).childen[c];
}
else
{
(*p).childen[c] = new Node;
p = (*p).childen[c];
for (int i = 0; i < 26; i++)
{
(*p).childen[i] = 0;
}
p->mark = 0;
}
}
p->mark = 1;
}
/** Returns if the word is in the trie. */
bool search(string word) {
PNode p = root;
int c = 0;
for (auto ch : word)
{
c = ch - 'a';
if ((*p).childen[c])
{
p = (*p).childen[c];
}
else
{
return false;
}
}
if (p->mark)
return true;
else
return false;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
bool startsWith(string prefix) {
PNode p = root;
int c = 0;
for (auto ch : prefix)
{
c = ch - 'a';
if ((*p).childen[c])
{
p = (*p).childen[c];
}
else
{
return false;
}
}
return true;
}
};
/**
* Your Trie object will be instantiated and called as such:
* Trie* obj = new Trie();
* obj->insert(word);
* bool param_2 = obj->search(word);
* bool param_3 = obj->startsWith(prefix);
*/
参考资料
[1] 向前走别回头.字典树(前缀树)[EB/OL].2018-08-24
https://blog.csdn.net/weixin_39778570/article/details/81990417
[2] GeeksforGeeks.Trie | (Insert and Search)[EB/OL].2019-09-04