题目链接:https://leetcode-cn.com/problems/contains-duplicate-iii/
这是个中等题?
题目
给你一个整数数组
nums和两个整数k和t。请你判断是否存在 两个不同下标i和j,使得abs(nums[i] - nums[j]) <= t,同时又满足abs(i - j) <= k。如果存在则返回
true,不存在返回false。示例1
- 输入: nums = [1,2,3,1], k = 3, t = 0
- 输出: true
示例2
- 输入: nums = [1,5,9,1,5,9], k = 2, t = 3
- 输出: false
数据范围
0 <= nums.length <= 2 * 104-231 <= nums[i] <= 231 - 10 <= k <= 1040 <= t <= 231 - 1
分析
朴素想法:遍历每个满足条件的 i 、 j ,找到符合条件的就退出。
时间复杂度 O(kn) ,直接超时。
想不到更优的办法了,查看题解之后在此进行记录。
Method 1、滑动窗口 + 有序集合
首先将问题进行简化。
- 希望使得
asb(i - j) <= k,那么我们每遍历到一个下标i,就直接 向前(向左) 查看k个元素,直到触及 左边界 。这样做的正确性在于,我们能够考虑到一个下标的左边k个元素,而它的右边k个元素在接下来的k轮循环中得以考虑。 - 希望使得
abs(nums[i] - nums[j]) <= t,化简绝对值不等式,等价于-t <= nums[i] - nums[j] <= t,等价于nums[i] - t <= nums[j] <= nums[i] + t。这个不等式表明了,对于一个nums[i]和它左边的k个元素 ,我们只需要考虑这k个元素中是否有一个落在nums[i] - t ~ nums[i] + t这个区间内。
对于第一点,希望保存这左边的 k 个元素,我们自然有许多种办法,但是普通的 队列、向量 等数据结构会使得第二点的条件难以实现 —— 我们如何在这 k 个元素中查找落在 nums[i] - t ~ nums[i] + t 区间内的元素呢?
显然,我们需要的是一种快速 查找 的数据结构,而且对于遍历到的一个 nums[i] 来说,我们还需要将其插入这个结构中,因此这个数据结构还需要实现快速的 插入 ,我们希望满足第二点要求,显然就需要这个数据结构是 有序的 ,这样查找一个特定范围内的数据才会显得方便。
好了,这样的数据结构就是 红黑树 。
很不幸地,我至今不会手写红黑树的实现;很幸运地,我们使用STL提供的类型就行了。
我此前写过的某篇文章也提及了,C++中 set / map / multiset / multimap 底层都是红黑树;具体到本题,使用 set 即可,因为在一段区间内出现两个相同元素的话,一定是满足条件的。
我们希望查找某个区间的元素,可以进一步转化为 一次查找 + 一次判断:对于一个 nums[i] ,我们找到 k 个元素中 第一个大于 nums[i] - t 的元素,判断其是否 小于 nums[i] + t ,若满足,返回 true ,若不满足,则这些元素中也没有其他的满足者。
记住,是 第一个大于 nums[i] - t 的元素!
非常不错地,set.lower_bound() 干的就是这份工作。
AC代码1
class Solution {
public:
bool containsNearbyAlmostDuplicate(vector<int>& nums, int k, int t) {
set<long> s;
// set.lower_bound(val)
// 返回集合中第一个 大于 val的元素
for (int i = 0; i < nums.size(); i++)
{
auto lb = s.lower_bound((long)nums[i] - t);
// cout << *lb << endl;cout << "I: " << i << endl;
if (lb != s.end() && *lb <= (long)nums[i] + t)
{
/*
cout << "I: " << i << endl;
cout << nums[i] << " " << t << endl;
cout << *lb << " <= " << (long)nums[i] - t << endl;
*/
return true;
}
s.insert((long)nums[i]);
if (i - k >= 0)
{
s.erase(nums[i - k]);
}
}
return false;
}
};
在上面的代码中,有几点需要注意:
- 数据类型! 这个题真是坑的不能再坑了,既然数据范围那么大的话,给出的输入数组就不要用
int嘛(手动擦汗)。我们的集合类型是long,每次加减法之前也都要将数据转为long。 - 删除范围外的数据。我们每一轮循环的时候是 先判断,再插入,再删除 ,因此注意边界条件是
i - k >= 0。
Method 2、桶排序
基本上所有的题解都说是桶排序,那我也就跟着说是桶排序吧,它的实际做法与我对桶排的认知还是有一定的区别的。
我们知道,在计算机中两个整型相除,结果还是整型,默认 向下取整 ,如 1 / 4 = 0 , 3 / 4 = 0 , 4 / 4 = 1 。
按照这样的逻辑,对于任意的两个 整数 n1 、 n2 ,若它们除以一个数 t 的结果相等,则 abs(n1 - n2) <= t - 1 。
我们使用反证法来进行证明:
已知
n1 ÷ t == n2 ÷ t,不妨令n1 > n2,设
abs(n1 - n2) > t - 1,则n1 > n2 + t - 1,即n1 >= n2 + t(它们都是整数);则
n1 ÷ t >= n2 ÷ t + 1,与已知条件违背,故当
n1 ÷ t == n2 ÷ t时,abs(n1 - n2) <= t - 1。
将这个定理结合题目进行分析,我们希望使得 abs(nums[i] - nums[j]) <= t ,若是 nums[i] / (t + 1) == nums[j] / (t + 1) ,则它们一定满足条件。
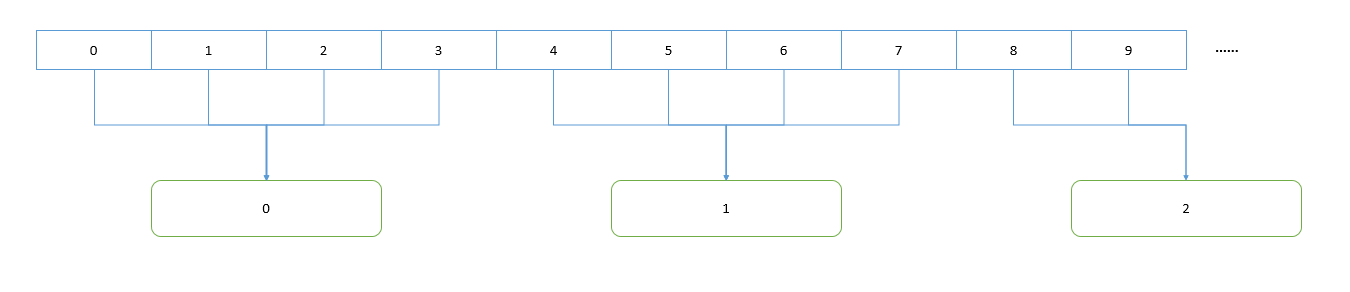
进行了理论上的证明,我们可以再来看看直观的模拟,设 t = 3 ,我们希望找到距离 不大于3 的一对数,根据上面的分析,我们应该计算 nums[i] / (3 + 1) 的值。
我们将下面的绿色框框称为 桶 ,上面的数字根据自己除以 4 的值来决定自己应该在哪一个桶里。非常容易发现,同一个桶中的数字满足 差的绝对值不大于3 这一要求。
除了同一个桶中的数字,显然相邻桶中的数字也可能满足要求。例如对于 1 号桶中的数字 5 来说,隔壁 0 号桶中的 3 或者隔壁 2 号桶中的 8 也是满足要求的。
我们对给出的整型数组进行遍历,得到一个数之后就去计算它所属的 桶编号 ,然后将这一对 桶编号 —— 数值 的映射保存起来。对于任意一个数,如果它的桶编号已经存在于我们的记录中,那么显然我们已经找到了 同一个桶中的两个数字 ,就可以 return true; 了;如果它的桶编号不存在于我们的记录中,我们还要看看它两边的桶是否存在,存在的话就取出其中的数值来比较一下大小,判断是否满足题意。
至此,仅剩最后一个细节了:负数。
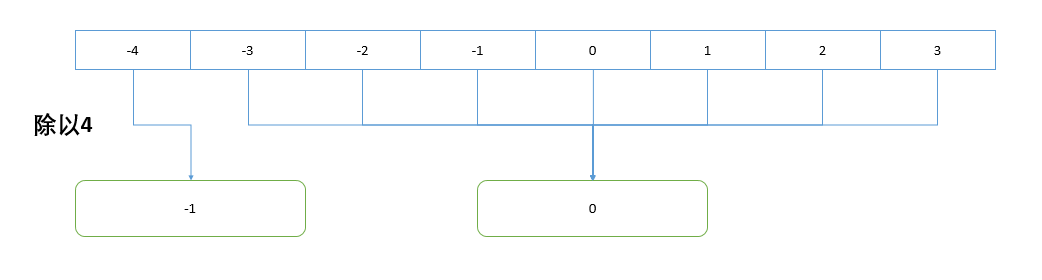
你会发现,引入了负数之后,如果还是计算 n / (t + 1) 的话,会出现一些尴尬的情况,还是以 t = 3 为例:
有几点问题:
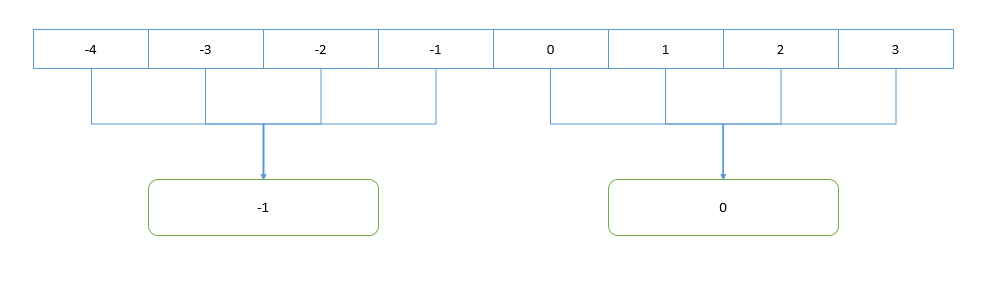
-3和3的计算结果竟然都是0,它们属于同一个桶,但是显然不符合abs(3 - (-3)) <= 3这一要求-4和-1 ~ -3的计算结果竟然是不一样的,但是-1 ~ -4显然应该属于同一个桶
我们一一来进行解决。
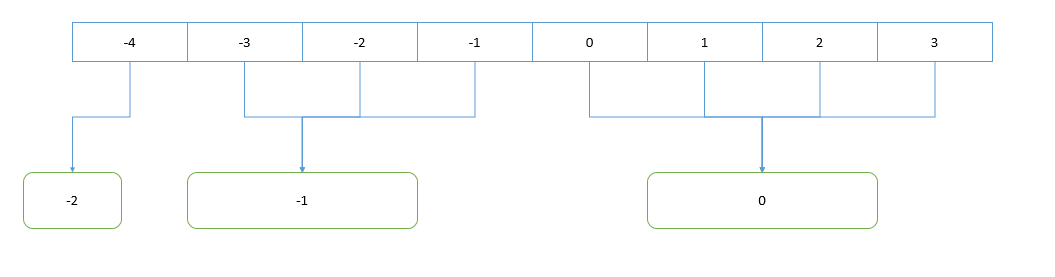
首先,负数和正数都可能计算出编号为 0 的桶,我们直接令 负数 的计算结果 减一 ,这样做对于我们的桶编号没有影响,但是可以把负数的计算结果和正数的计算结果分开。
其次,我们已经将 0 ~ 3 归于正整数的计算中了(0号桶),则不必再将 0 放入到负数的队伍中;这样来说,全体负数应该先 加上1 再进行计算,补上 0 的位置。
这样, -1 ~ -4 就都属于同一个桶中了。
综合以上分析,我们在具体实现中使用一个 map<int, int> 来保存 桶编号 —— 数值 这一映射,遍历数组,计算对应数值的桶编号,查看 map 中是否已经有了相同编号或相邻编号的桶;根据题意,我们一次只能保存 k 个桶,那么只需要重新计算边界数值对应的桶编号,将其删除之后再继续进行循环。
AC代码2
class Solution {
public:
int getID(int n, int t)
{
if (n >= 0)
{
return (long)n / ((long)t + 1);
}
else
{
return ((long)n + 1) / ((long)t + 1) - 1;
}
}
bool containsNearbyAlmostDuplicate(vector<int>& nums, int k, int t) {
map<int, int> bucket;
for (int idx = 0; idx < nums.size(); idx++)
{
int id = getID(nums[idx], t);
// cout << id << endl;
auto ite = bucket.find(id);
if (ite != bucket.end())
{
if (abs((long)nums[idx] - ite->second) <= t)
return true;
}
ite = bucket.find(id - 1);
if (ite != bucket.end())
{
if (abs((long)nums[idx] - ite->second) <= t)
return true;
}
ite = bucket.find(id + 1);
if (ite != bucket.end())
{
if (abs((long)nums[idx] - ite->second) <= t)
return true;
}
bucket[id] = nums[idx];
if (idx - k >= 0)
{
ite = bucket.find(getID(nums[idx - k], t));
bucket.erase(ite);
}
}
return false;
}
};
表现烂爆,就不放图了。一些题解中使用 map.count() 来判断桶是否存在,我使用 map.find() ,这样代码就冗长了一些。不过既然本题的核心算法实现了,其余细节了解便好。
参考资料
[1] 力扣官方题解.存在重复元素 III[EB/OL].2021-04-17
[2] 宫水三叶.【宫水三叶】一题双解:「滑动窗口 & 二分」&「桶排序」解法[EB/OL].2021-04-17
[3] 黎猫大侠.C++利用桶分组,详细解释[EB/OL].2021-04-17